Informática Educativa I :: Projeto de
Aprendizagem
|
Título: A importância do Tangram no ensino da Matemática
|
Nome
do Aluno: Sandra Cristina Rodrigues Pimentel
|
1. Disciplina e anos envolvidos:
|
2. Tema central :
A importância do Tangram no ensino da Geometria
|
3. Temas de apoio:
- Geometria
Plana
- Geometria Dinâmica
- A
história do Tangram
- Figuras geométricas planas
- Razão, Proporção e Semelhança
|
4. Justificativa:
A escolha
deste tema deve-se a intenção de proporcionar uma aula mais agradável e
motivadora aos nossos educandos, utilizando ferramentas tecnológicas da Web
2.0, favorecendo a aprendizagem. Utilizando o software Régua e Compasso, visa
provocar a incorporação do hábito de uso de softwares de visualização aos
alunos, explorando a interação entre eles através do trabalho em duplas
para que assim se envolvam mais, aperfeiçoando uma socialização maior entre eles.
Trabalhando com materiais concretos e ferramentas da Web, mostraremos a
Matemática com uma nova visão.
Com este
trabalho, pretende-se mostrar aos alunos a importância e o quanto é útil em
nosso dia-a-dia a Geometria Plana, visando despertar em nosso educando o
interesse pela Matemática e pelo conteúdo proposto, envolvendo-os em situações
reais, proporcionando motivação e contribuindo assim para a aprendizagem da
aplicação do mesmo, através de situações que despertem o interesse do aluno,
através da construção do Tangram.
Além do
aspecto lúdico do jogo, o Tangram pode ser explorado no ensino da Matemática.
Ele pode ser utilizado em diferentes conteúdos como área, perímetro, razão,
proporção, fração, multiplicação, divisão, semelhança, simetrias, transformações
isométricas, etc. Pode ser explorado também em interdisciplinaridade com as
Ciências, Artes e História. São inúmeras as possibilidades exploratórias do
Tangram utilizando-se de material concreto de manipulação. No entanto, o uso do
ambiente computacional pode ampliar ainda mais as potencialidades pedagógicas
do Tangram.
Dentre os
diversos softwares que podem ser utilizados com o Tangram, destacamos os de
Geometria Dinâmica, neste projeto, utilizaremos o software Régua e Compasso. Os
alunos poderão usar técnicas de desenho geométrico para construir as peças do
Tangram. Pode-se usar ferramentas para medir distâncias e ângulos, área,
perímetro, estabelecer ou verificar relações, propriedades etc.
A
decomposição e composição de figuras geométricas constituem uma atividade
lúdica e permitem um melhor conhecimento das suas propriedades e das relações
entre os seus elementos.
|
5. Objetivos gerais e específicos:
Objetivo Geral:
. Realizar diversas atividades utilizando o Tangram com os recursos da Web
2.0, num ambiente colaborativo de aprendizagem.
Objetivos específicos:
. Proporcionar ao aluno atividades
lúdicas e desafiadoras;
. Proporcionar uma aula agradável
aos alunos, utilizando o computador;
. Demonstrar as utilidades do software Régua e Compasso na Geometria Dinâmica;
. Mostrar através da dinâmica, dentro do software Régua e Compasso, a
formação do Tangram;
. Despertar a criatividade dos alunos, ao verificar o que podemos fazer
utilizando o Tangram;
. Apresentar algumas maneiras de integrar as potencialidades didáticas do
Tangram com a da geometria dinâmica;
. Identificar e reconhecer elementos das figuras geométricas planas;
. Agregar materiais que estimulem a curiosidade, a observação, a
investigação e a troca de experiências e vivências;
. Desenvolver o raciocínio lógico para a resolução de problemas e
habilidades na utilização dos materiais a serem utilizados;
. Incentivar o gosto pela Matemática e o desenvolvimento do raciocínio
lógico;
|
6. Enfoque pedagógico :
Nosso enfoque pedagógico é
Construtivista, pois envolve construção, pesquisa e cooperação de todos os
envolvidos. O aluno é o sujeito ativo no processo de aprendizagem, através da
experimentação, da pesquisa em grupo, do estímulo à dúvida e ao desenvolvimento
do raciocínio. O professor será um mediador e facilitador do processo em
desenvolvimento do aluno e um estimulador para a realização das atividades, onde
os alunos pesquisarão sobre o assunto e sua história e irão construir o seu
próprio Tangram.
|
7. Recursos tecnológicos:
. Computadores com acesso a internet e
recursos da web 2.0 (Blog, vídeos, slideshare, objetos de aprendizagem).
. Uso de sites de busca para pesquisas.
. Computadores que tenham o software Régua e Compasso instalado ou que se possa baixar da internet. Site: http://www.professores.uff.br/hjbortol/car/programs/jre-6u5-windows-i586-p-s.exe.
|
8. Etapas e suas
estratégias de realização:
- Apresentação do tema.
- Dividir a turma em duplas.
- Pesquisar
sobre o tema: Tangram.
- Construção do Tangram.
- Manipulação
do Tangram.
- Criação de
Blog.
-
Apresentação e exposição dos resultados.
- Avaliação
do trabalho.
|
9. Definição de papéis:
No primeiro
momento os alunos serão pesquisadores, fazendo suas buscas e colhendo suas
informações.
Após este momento,
os alunos serão os construtores do conhecimento, construindo o Tangram, através
de papel, desenhos e recortes, e através do software Régua e Compasso, onde
postarão os seus trabalhos num blog criado por eles.
O professor,
durante todo o projeto será o orientador e mediador das pesquisas, de tal forma
que os alunos construam seus próprios conhecimentos.
|
10. Sites e bibliografia de apoio:
CARROCINO, Carlos Homero Gonçalves; GARCIA, Fábio Luiz
Machry Rodrigues; SILVA, Sérgio Ferreira; CARVALHO; Teresa Cristina Medeiros. O Tangram no Ensino da Matemática. Disponível
em: <http://www.slideshare.net/tecrim/projeto-pedaggico-apresentao>.
Acesso em: 21/10/2012.
História do Tangram. Disponível em: <http://proportoseguro.blogspot.com.br/2009/03/historia-do-tangran.html>. Acesso em: 26/10/2012.
KERCHE, Luciana. Figuras
para montar com o Tangram. Disponível em: <http://lucianakerche.blogspot.com.br/2011/03/figuras-para-montar-com-o-tangram.html>.
Acesso em: 25/10/2012.
MATTOS, Anderson Santos. Trabalhando Geometria com o Tangram. Disponível em: <http://www.ebah.com.br/content/ABAAAA41oAI/trabalhando-geometria-com-tangram>.
Acesso em: 20/10/2012.
Régua e
Compasso. Disponível em: <http://www.professores.uff.br/hjbortol/car/programs/jre-6u5-windows-i586-p-s.exe.>. Acesso em 20/10/2012.
Um passeio
regional com os números: da história antiga aos dias atuais! Disponível em:
<http://atitudenamatematica.blogspot.com.br/2009/06/informatica-educativa-ii-projeto-de.html>.
Acesso em: 20/10/2012.
|
11. Coleta de dados:
Pesquisa em sites
de busca e alguns livros didáticos.
|
12. Seleção do material:
- Site de busca,
para pesquisar a história e a importância do Tangram para a Matemática.
- Papel, tesoura e
lápis de cor, para a construção do Tangram.
- Software Régua e
Compasso, para a construção do Tangram.
- Blog.
|
13. Programação visual:
A turma, dividida
em duplas, postarão suas pesquisas e a construção do Tangram, através de um
blog criado por eles.
|
14. Meios para a execução:
- Utilização do
laboratório de informática para pesquisa e composição dos trabalhos para
apresentação e confecção do blog.
- Software Régua e
Compasso.
- Blog, para
apresentação da culminância do projeto.
|
15. Avaliação:
Serão avaliados o
comportamento do aluno, seu interesse, empenho e dedicação ao realizar as
atividades. A avaliação acontecerá
durante o desenvolvimento de todas as etapas do projeto, não tendo como
objetivo controlar ou qualificar os educandos, mas ajudá-los a progredirem na
busca do conhecimento. O produto final, postado no blog, também será avaliado
para tomada de consciência do que foi aprendido, permitindo reconhecer se os
alunos alcançaram o resultado esperado.
|
16. Cronograma:
Nosso projeto terá
2 semanas para ser concretizado. Cada aula será representada por 2 tempos de 50
minutos cada e cada semana terá 6 tempos de aula.
Seguindo a
seguinte organização:
- 1ª aula:
- Inicialmente o
professor introduzirá o assunto Tangram com os alunos, dividirá a turma em
duplas e apresentará o Tangram.
- Início das
pesquisas. O aluno irá pesquisar em sites na internet, sobre a origem e
importância do Tangram para a Matemática.
- 2ª aula:
- Conclusão das
pesquisas, análise do material e debate sobre a importância do Tangram para a
Matemática.
História do Tangram
Tangram é um quebra-cabeça chinês formado por 7 peças (5 triângulos, 1 quadrado
e 1 paralelogramo).
Com essas peças pode-se formar várias figuras, utilizando todas elas sem
sobrepô-las. Segundo a Enciclopédia do Tangram é possível montar mais de 1700
figuras com as 7 peças.
Esse quebra-cabeça, também conhecido como jogo das sete peças, é
utilizado pelos professores de matemática como instrumento facilitador da
compreensão das formas geométricas. Além de facilitar o estudo da Geometria, ele
desenvolve a criatividade e o raciocínio lógico, que também são fundamentais
para o estudo da Matemática.
Não se sabe ao certo como surgiu o Tangram, apesar de haver várias
lendas sobre sua origem.
Lendas:
"Era uma vez, num país muito distante, um senhor chinês chamado
Tan. O senhor Tan vivia num palácio dourado, junto de um lago. O que ele mais
adorava era passear à volta do lago durante horas a fio... Um dia, enquanto caminhava,
viu no chão um objeto brilhante. Baixou-se e descobriu um magnífico azulejo de
prata. Apanhou-o e admirou-o: o azulejo era liso como a superfície do lago,
macio como uma pluma, brilhante como o seu traje. Quis virá-lo mas...
infelizmente, o lindo azulejo escapou-lhe das mãos e partiu-se no chão em 7
pedaços! O senhor Tan, desiludido, tentou reconstituí-lo. Juntando as peças,
criou a forma de uma pequena personagem! Deslocou mais umas peças e, para seu
espanto, formou-se uma linda casa! O senhor Tan regressou ao palácio muito entusiasmado
por ter inventado um novo jogo. Batizou-o de TANGRAM e mandou fabricar um para
cada habitante do seu reino!"
“Um jovem chinês, ao despedir-se do seu mestre para uma grande viagem
pelo mundo, recebeu um espelho de forma quadrada e ouviu:
- Com esse espelho, registarás tudo o que vires durante a viagem, para
mostrar-me na volta.
O discípulo, surpreendido, perguntou:
- Mas mestre, como, com um simples espelho, poderei eu mostrar-lhe tudo
o que encontrar durante a viagem?
No momento em que fez esta pergunta, o espelho caiu-lhe das mãos
quebrando-se em sete peças. Então o mestre disse:
- Agora poderás, com essas sete peças, construir figuras para ilustrar
o que vires durante a viagem.”
“Uma pedra preciosa se desfez em sete pedaços, e com elas era possível
formar várias formas, tais como animais , plantas e pessoas.”
Segundo alguns, o nome Tangram vem da palavra inglesa
"trangam", de significado "puzzle" ou
"buginganga". Outros dizem que a palavra vem da dinastia chinesa
Tang, ou até do barco cantonês "Tanka", onde mulheres entretinham os
marinheiros americanos. Na Ásia o jogo é chamado de "Sete placas da
Sabedoria".
- 3ª aula:
- Construção do
material: Aprendendo a construir um Tangram. Após a Construção do Jogo de
Tangram, o professor usará essa demonstração, revisando conceitos matemáticos,
tais como: Razão, Proporção e Semelhança.
- 4ª aula:
- Os alunos
poderão manipular as peças, podendo construir várias figuras, através das
figuras geométricas do Tangram.
Atividades:
Utilizando as
peças do Tangram:
1-
Monte uma figura
com as 7 peças sem sobrepô-las.
2-
Monte um quadrado
com 3 triângulos.
3-
Monte um quadrado
com 4 peças.
4- Monte um
quadrado com 5 peças.
Exemplos de
figuras que poderão ser formadas com o Tangram:
- 5ª aula:
- Continuação da
construção do Tangram, agora utilizando o software Régua e Compasso, onde eles
também poderão manipular as figuras através deste software de Geometria
Dinâmica.
Para fazer um
Tangram no Software Régua e Compasso:
Construir um
Tangram a partir de um quadrado com 6 cm de lado.
Com a ferramenta
SEGMENTO, construir um segmento medindo 6 cm:
Com a ferramenta
PERPENDICULAR, traçar duas perpendiculares pontilhadas a esse segmento:
Com a ferramenta
COMPASSO, marcar nos 2 pontos do segmento, as circunferências. Traçar um ponto
de intersecção e com a mesma abertura, traçar o outro ponto perpendicular.
Com a ferramenta
SEGMENTO, traçar os segmentos, ligando os pontos formando um quadrado:
Com a ferramenta
SEGMENTO, traçar uma diagonal:
Traçar esta
diagonal em 4 partes iguais. Utilizando a ferramenta PONTO MÉDIO, dividí-la ao
meio.
Dividir as duas
metades ao meio, através da ferramenta PONTO MÉDIO:
Com a ferramenta
PONTO MÉDIO, dividir ao meio também duas das laterais:
Unir, através da
ferramenta SEGMENTO, os pontos médios das duas laterais:
Através da
ferramenta PONTO MÉDIO, dividir este segmento ao meio:
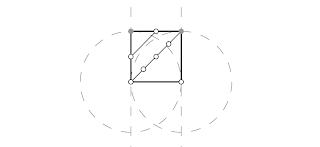
Através da
ferramenta SEGMENTO, unir os pontos:
Com a ferramenta
OCULTAR OBJETO, ocultar os segmentos e as circunferências pontilhadas:
Pronto! O nosso
Tangram já está pronto para imprimir e recortá-lo e assim fazer várias figuras
com ele.
- 6ª aula:
- Os alunos, em
duplas, criarão um blog, onde postaram as diversas tarefas e pesquisas realizadas.
|
domingo, 28 de outubro de 2012
A importância do Tangram no Ensino da Matemática
Assinar:
Postar comentários (Atom)

















Nenhum comentário:
Postar um comentário